3.2 KiB
3.2 KiB
二次函数 y = -2x^2 + 8x - 3 顶点与最值 - 求解报告
1. 🎯 问题描述
已知二次函数 $y = -2x^2 + 8x - 3$,求:
- 函数的顶点坐标
- 函数的最大值
2. ✅ 最终结论
对于二次函数 $y = -2x^2 + 8x - 3$:
顶点坐标为 $(2, 5)$。由于二次项系数 $a = -2 < 0$,抛物线开口向下,因此函数在顶点处取得最大值 $y_{max} = 5$,此时 $x = 2$。
换句话说,当 x = 2 时,函数值达到最大,为 $5$;当 x 偏离 2 时(无论向左还是向右),函数值都会减小。
3. 📈 可视化
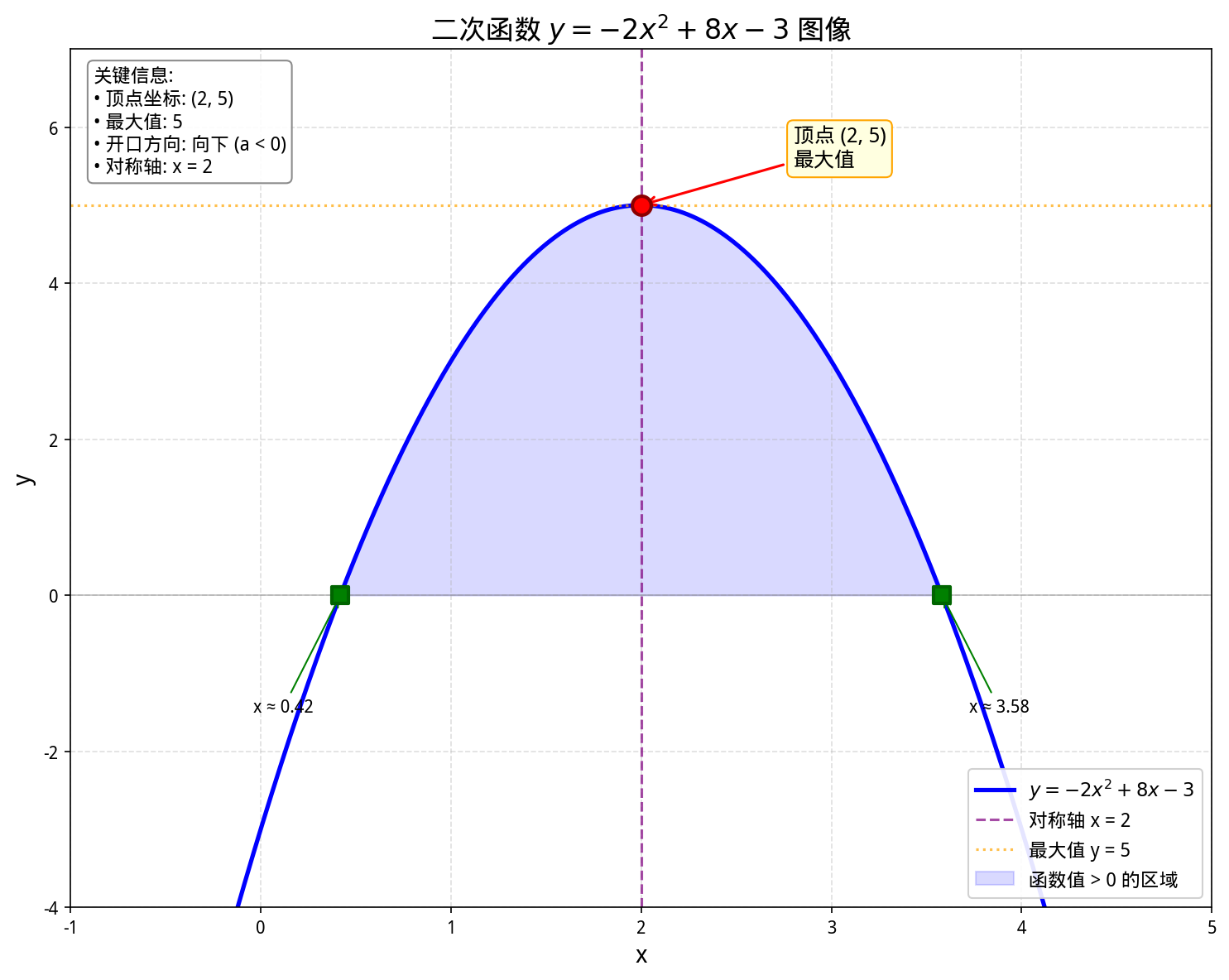
图表说明:
- 蓝色曲线:二次函数
y = -2x^2 + 8x - 3的图像 - 红色圆点:顶点 $(2, 5)$,即函数的最高点
- 绿色方块:函数与
x轴的两个交点(零点) - 紫色虚线:对称轴
x = 2 - 橙色点线:最大值参考线
y = 5 - 浅蓝色区域:函数值大于零的区域
4. 🧠 数学建模与解题过程
点击展开
问题分析:这是一个关于二次函数顶点和最值的基本问题。对于一般形式的二次函数 $y = ax^2 + bx + c$,其图像是一条抛物线,顶点坐标和最值可以通过多种方法求解。
方法选择:本题采用三种方法相互验证:
方法一:顶点公式
对于 $y = ax^2 + bx + c$,顶点坐标为:
\left( -\frac{b}{2a}, \frac{4ac - b^2}{4a} \right)
本题中 $a = -2$,$b = 8$,$c = -3$,代入得:
x_{顶点} = -\frac{8}{2 \times (-2)} = -\frac{8}{-4} = 2
y_{顶点} = \frac{4 \times (-2) \times (-3) - 8^2}{4 \times (-2)} = \frac{24 - 64}{-8} = \frac{-40}{-8} = 5
方法二:求导法
对函数求导:
y' = \frac{d}{dx}(-2x^2 + 8x - 3) = -4x + 8
令 $y' = 0$,解得 $x = 2$。
将 x = 2 代入原函数:y = -2(2)^2 + 8(2) - 3 = -8 + 16 - 3 = 5
方法三:配方法
y = -2x^2 + 8x - 3
= -2(x^2 - 4x) - 3
= -2(x^2 - 4x + 4 - 4) - 3
= -2(x - 2)^2 + 8 - 3
= -2(x - 2)^2 + 5
顶点式为 $y = -2(x - 2)^2 + 5$,直接读出顶点 $(2, 5)$。
结论:三种方法结果一致,顶点为 $(2, 5)$。由于 $a = -2 < 0$,抛物线开口向下,函数在 x = 2 处取得最大值 $5$。
5. 📊 运行结果
点击展开
==================================================
二次函数 y = -2x² + 8x - 3 求解
==================================================
【方法1:顶点公式】
a = -2, b = 8, c = -3
顶点横坐标 x = -b/(2a) = -8/(2×-2) = 2.0
顶点纵坐标 y = (4ac-b²)/(4a) = 5.0
【方法2:SymPy 求导验证】
y' = 8 - 4*x
令 y' = 0,解得 x = [2]
将 x = 2 代入原函数:y = 5
【方法3:配方法】
y = -2x² + 8x - 3
= -2(x² - 4x) - 3
= -2(x² - 4x + 4 - 4) - 3
= -2(x - 2)² + 8 - 3
= -2(x - 2)² + 5
顶点形式:y = -2(x - 2)² + 5
==================================================
【最终结果】
==================================================
顶点坐标:(2, 5)
由于 a = -2 < 0,抛物线开口向下
函数最大值:y_max = 5(在 x = 2 处取得)