# 二次函数 $y=-2x^2+8x-3$ 求解报告

## 1. 🎯 问题描述

已知二次函数 $y=-2x^2+8x-3$，求：
1. 函数的顶点坐标
2. 函数的最大值

## 2. ✅ 最终结论

该二次函数的顶点坐标为 $(2, 5)$。
由于二次项系数 $-2 < 0$，抛物线开口向下，函数在顶点处取得最大值，最大值为 $5$。

## 3. 📈 可视化

![函数图像](figure.png)

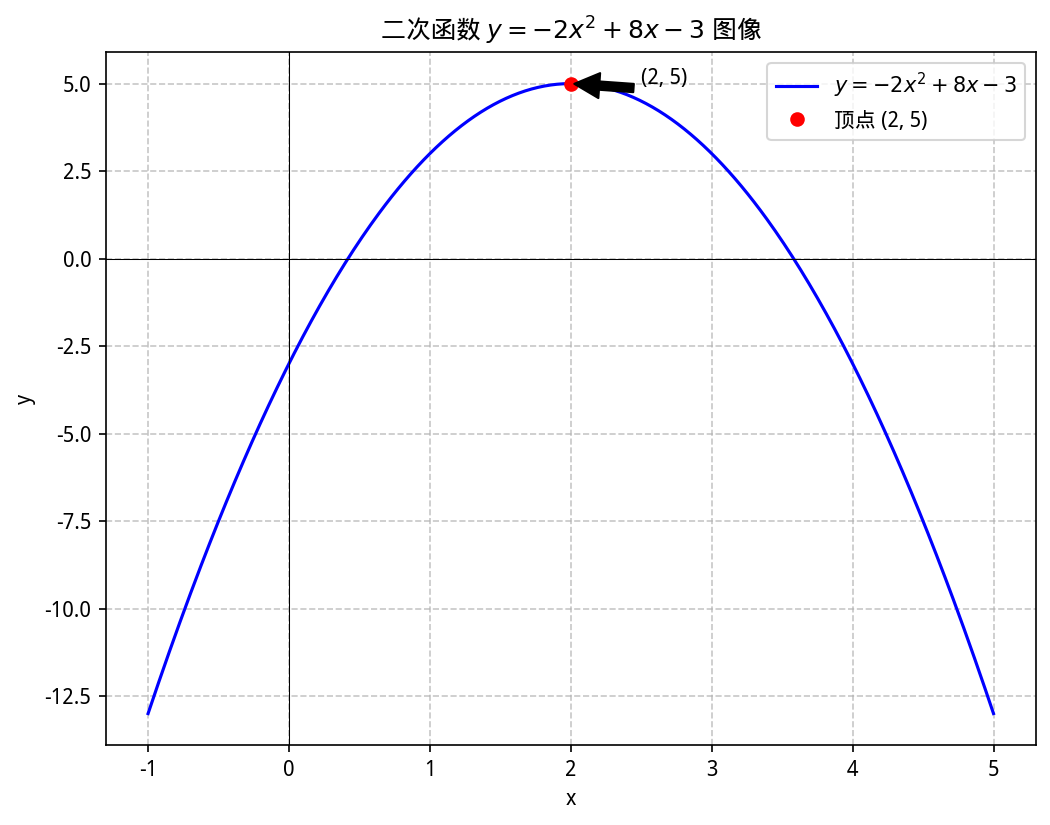
**图表说明**：
- 蓝色曲线：二次函数 $y = -2x^2 + 8x - 3$ 的图像
- 红色圆点：函数的顶点 $(2, 5)$，也是函数的最高点

## 4. 🧠 数学建模与解题过程

<details>
<summary><strong>点击展开</strong></summary>

**问题分析**：
这是一个标准的二次函数性质分析问题。二次函数的一般形式为 $y = ax^2 + bx + c$。
本题中，$a = -2, b = 8, c = -3$。

**方法选择**：
可以通过配方法将一般式转化为顶点式 $y = a(x-h)^2 + k$，从而直接读出顶点 $(h, k)$ 和最值。
也可以利用导数法求极值点。
这里我们使用 SymPy 进行符号计算，通过求导数的方法来确定顶点和最值。

**推导过程**：

1.  **求导数**：
    对 $y = -2x^2 + 8x - 3$ 关于 $x$ 求导：
    $$ \frac{dy}{dx} = -4x + 8 $$

2.  **求驻点**：
    令导数为 0，解方程：
    $$ -4x + 8 = 0 \implies x = 2 $$

3.  **求顶点坐标**：
    将 $x = 2$ 代入原函数求 $y$：
    $$ y = -2(2)^2 + 8(2) - 3 = -8 + 16 - 3 = 5 $$
    所以顶点坐标为 $(2, 5)$。

4.  **判断最值**：
    计算二阶导数：
    $$ \frac{d^2y}{dx^2} = -4 $$
    因为二阶导数小于 0，说明该驻点是极大值点。
    对于二次函数，极大值即为全局最大值。

</details>

## 5. 📊 运行结果

<details>
<summary><strong>点击展开</strong></summary>

```
Critical points (x): [2]
Vertex: (2, 5)
Second derivative: -4
The vertex is a maximum.
Maximum value: 5
```

</details>