# 二次函数 $y=-2x^2+8x-3$ 求解报告
## 1. 🎯 问题描述
已知二次函数 $y = -2x^2 + 8x - 3$,求:
1. 函数的顶点坐标
2. 函数的最大值
## 2. ✅ 最终结论
这个二次函数的开口向下(因为 $a = -2 < 0$),所以它有一个最高点。通过顶点公式计算,顶点坐标为 $(2, 5)$,这也是函数的最大值点。也就是说,当 $x = 2$ 时,函数取得最大值 $y = 5$。
## 3. 📈 可视化
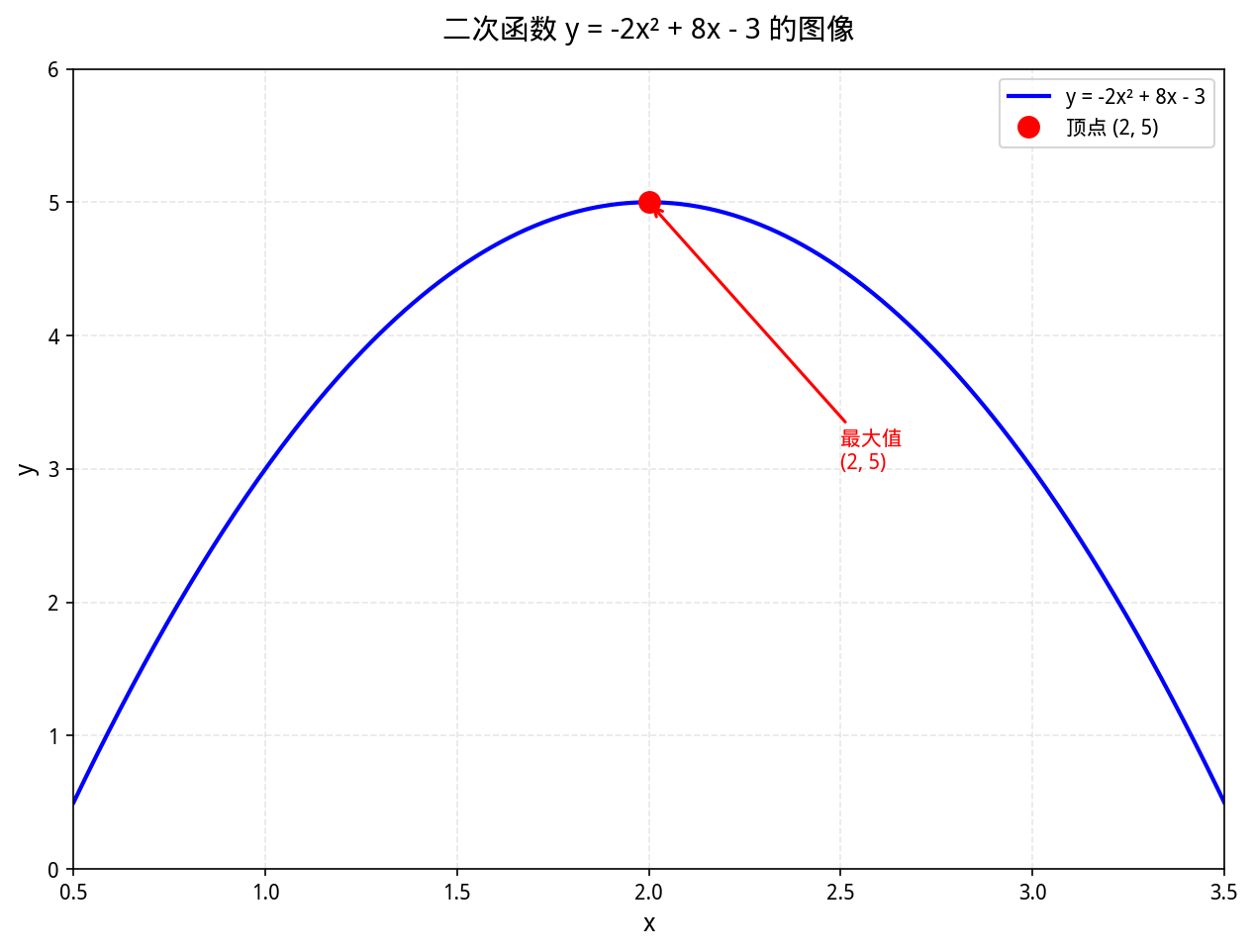
**图表说明**:
- 蓝色曲线:函数 $y = -2x^2 + 8x - 3$ 的图像
- 红色圆点:函数的顶点 $(2, 5)$,即最大值点
从图像中可以清晰地看到,抛物线开口向下,在 $x = 2$ 处达到最高点,对应 $y = 5$。
## 4. 🧠 数学建模与解题过程
点击展开
### 问题分析
这是一个关于二次函数性质的问题。对于一般形式的二次函数 $y = ax^2 + bx + c$,其图像是一条抛物线。我们需要:
1. 找到抛物线的顶点坐标
2. 确定函数的最大值(如果存在)
### 方法选择
本题可以采用两种方法求解:
**方法一:顶点公式法**
二次函数 $y = ax^2 + bx + c$ 的顶点坐标为:
$$x = -\frac{b}{2a}, \quad y = f\left(-\frac{b}{2a}\right)$$
**方法二:求导法**
对函数 $y = ax^2 + bx + c$ 求导:
$$y' = 2ax + b$$
令 $y' = 0$,解得临界点:
$$x = -\frac{b}{2a}$$
再通过二阶导数 $y'' = 2a$ 判断极值性质:
- 当 $a > 0$ 时,$y'' > 0$,为极小值点
- 当 $a < 0$ 时,$y'' < 0$,为极大值点
### 推导过程
**使用顶点公式法**:
已知 $a = -2$,$b = 8$,$c = -3$
1. 顶点的 x 坐标:
$$x = -\frac{b}{2a} = -\frac{8}{2 \times (-2)} = -\frac{8}{-4} = 2$$
2. 顶点的 y 坐标(将 $x = 2$ 代入原函数):
$$y = -2 \times 2^2 + 8 \times 2 - 3 = -2 \times 4 + 16 - 3 = -8 + 16 - 3 = 5$$
因此,顶点坐标为 $(2, 5)$。
**使用求导法验证**:
1. 求一阶导数:
$$y' = \frac{d}{dx}(-2x^2 + 8x - 3) = -4x + 8$$
2. 令 $y' = 0$,解得临界点:
$$-4x + 8 = 0 \Rightarrow x = 2$$
3. 求二阶导数:
$$y'' = \frac{d}{dx}(-4x + 8) = -4$$
4. 由于 $y'' = -4 < 0$,所以 $x = 2$ 是极大值点。
5. 将 $x = 2$ 代入原函数:
$$y = -2 \times 2^2 + 8 \times 2 - 3 = 5$$
两种方法得到相同的结果。
### 最大值分析
因为 $a = -2 < 0$,抛物线开口向下,所以顶点处的 y 值就是函数的最大值。
$$y_{\text{max}} = 5$$
## 5. 📊 运行结果
点击展开
```
==================================================
二次函数:y = -2x² + 8x - 3
==================================================
【方法1:顶点公式】
顶点坐标:(2.0, 5.0)
【方法2:求导法】
导数:y' = 8 - 4*x
二阶导数:y'' = -4
临界点:x = 2
代入原函数:y = 5
二阶导数:-4 < 0,故为极大值点
【结论】
1. 顶点坐标:(2.0, 5.0)
2. 函数最大值:5.0
```